Rules of Exponents: “Used to Think” Method
| Lesson Objectives | For this lesson, students are learning to combine rules of exponents to simplify expressions. This activity was created to reveal student misconceptions about exponential expressions, and to cause students to critically think about exponents. This activity encourages students to think about their individual rules for exponents, as well as the “why” behind each rule.
Although students will be problem solving with a partner, at the end of the activity they will reflect upon what they used to think about exponents, and what they now know following the activity. |
| Lesson Standards | CCSS.MATH.CONTENT.8.EE.A.1 Know and apply the properties of integer exponents to generate equivalent numerical expressions. For example, 32 × 3-5 = 3-3 = 1/33 = 1/27.
CCSS.MATH.PRACTICE.MP2 Reason abstractly and quantitatively. CCSS.MATH.PRACTICE.MP3 Construct viable arguments and critique the reasoning of others. CCSS.MATH.PRACTICE.MP5 Use appropriate tools strategically. CCSS.MATH.PRACTICE.MP7 Look for and make use of structure. CCSS.MATH.PRACTICE.MP8 Look for and express regularity in repeated reasoning. |
| Prior Knowledge | This lesson is intended for a 7th or 8th grade classroom in which students are first introduced to exponent rules.
Prior to this lesson, students have learned order of operations, and the following exponent rules: multiplying powers with the same base, power of a product, and power of a power. |
| Why Use the “Used to Think” Method? | When teaching rules of exponents, many misconceptions can arise. The goal of this activity is to cause students to identify some of their misconceptions, learn from their mistakes, and understand the content at a deeper level. The “Used to Think” method allows students first to learn from their mistakes, but also become more aware of how their level of understanding changes as they critically think about a topic. |
| Materials and Set-Up | Materials:
Set-Up: In this lesson, students will be working with partners to match unsimplified exponential expressions to their corresponding simplified expressions. The teacher should copy and cut the exponential expression cards seen below, and will put the set of cards in an envelope. Each group of students will receive one envelope containing the set of 10 cards. Many of the expressions below have similar simplified expressions, which will encourage students to think critically about how exponential expressions are simplified.
|
| Outline | (1) The teacher will pass out a set of cards to each group, and will explain that the students’ goal is to match an unsimplified expression to a simplified expression.
Note: If students struggle to understand what is meant by simplifying expressions, the teacher can provide some insight by comparing simplifying expressions to simplifying sentences in English class. The following is an example of simplifying sentences: “You and I should both get in the car and go to the grocery store at the end of the street to pick up icecream.” “Let’s go get icecream at Kroger.” Clearly, the second sentence is much simpler. This example would help students to understand the difference between unsimplified and simplified expressions, as well as the value in simplifying expressions. Another example the teacher can use to help students understand the importance of simplifying expressions can be found here. (2) Students will discuss with their partners and try to match the expressions. Note: Many different conversations and misconceptions will arise as students look at the matching cards. For example, some students may struggle to identify the difference between an unsimplified and simplified expression, which could lead to conversations about what makes an expression simplified. Some students may match incorrectly because they mix up when they should add exponents and when they should multiply. This may lead to conversations of how it is important to understand “why” the rules work the way they do (exponents are repeated multiplication), and not just what the rules are. (3) After completing the task, students will check in with the teacher, and if they make any mistakes will be asked to correct their matches. (4) Once students complete the assignment, the teacher will lead students into the “Used to Think” portion of the lesson. A sample script is given below. “Before this activity, you all had some ideas of how to simplify expressions with exponents. I want you to write down a few sentences about what you used to think about expressions with exponents. “ [The teacher should give students plenty of time to process and write.] “Now I want you to think about how your ideas about exponents have changed after this activity. Again, write down a few sentences and what you now think about expressions with exponents.” [Again, the teacher should give students plenty of time to process and write.] (5) Once students have written what they used to think and now think, the teacher can ask students to share their change in thinking with the class. The teacher should look for ways to ask questions and push students to think about the content at a more critical level. Notes:
|
| Lesson Extension | As an extension for the lesson, students can create their own sets of 5 matching cards. Students should be sure to include examples that address all of the rules they have learned so far (multiplying powers with the same base, power of a product, and power of a power) in their cards. This extension allows for students to synthesize what they have learned, and therefore leads to more reflection and a deeper level of understanding. It also creates a space for students to reflect upon what they have learned throughout the lesson.
The teacher can also use this video as a reteach and preview of future rules if desired: Exponent Song |
| Assessment | Formative assessments:
Summative assessment:
|
Circumference of Circles: “See, Think, Wonder” Method
| Lesson Objectives | The goal of this lesson is for students to recognize the relationship between the circumference of a circle and either its radius or diameter. Following this lesson, students should be able to identify that the ratio of the circumference to the diameter is pi, and the ratio of circumference to radius is pi. Following the lesson, students should also recognize that if they know the radius or diameter of a circle, they can then find the circumference. |
| Standards | CCSS.MATH.CONTENT.7.G.B.4 Know the formulas for the area and circumference of a circle and use them to solve problems; give an informal derivation of the relationship between the circumference and area of a circle.
CCSS.MATH.PRACTICE.MP2 Reason abstractly and quantitatively. CCSS.MATH.PRACTICE.MP3 Construct viable arguments and critique the reasoning of others. CCSS.MATH.PRACTICE.MP4 Model with mathematics. CCSS.MATH.PRACTICE.MP5 Use appropriate tools strategically. CCSS.MATH.PRACTICE.MP7 Look for and make use of structure. CCSS.MATH.PRACTICE.MP8 Look for and express regularity in repeated reasoning. |
| Prior Knowledge | The target audience of this lesson is 7th grade students.
Before this lesson, students have learned basic circle vocabulary (circumference, radius, diameter), but have not performed any area or circumference explorations. Most students have also heard of and know that it is approximately 3.14, but do not know that pi is the ratio of circumference to diameter. |
| Why Use the “See, Think, Wonder” Method? | This lesson is an introduction into relating radius and diameter to the circumference of a circle. The goal for students is to view the radius, diameter, and circumference of each circle, think about how these measurements relate, and then wonder if this relationship occurs in all cases, and how it can be used in future cases. |
| Materials and Set-Up | Materials:
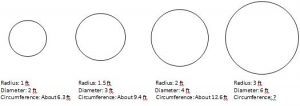
Set-Up: Before students come in the room, the teacher should draw or project images of four circles of differing size on the board. Below the first three circles, the teacher should record measurements of circumference, radius, and diameter. Below the fourth circle, the teacher should write the diameter, but leave circumference blank. An example of this is given below.
|
| Outline | (1) When students come in, the teacher should explain that he or she measured the radius and the diameter of the circles using a ruler, and then used measuring tape to find the circumference. The teacher can then say, “Notice that on the third circle, the circumference is not given. Our goal today is to figure out what it would be without measuring.
(2) See: Ask students to independently write down what they see looking at the first three circles (Note: This step can be done as a “Think-Pair-Share” with a partner.). After students write something down, have them share with the class what they see. (3) Think: Ask students to independently write what they think is happening with the circles (Note: This step can also be done as a “Think-Pair-Share” with a partner.). After students write something down, have them share with the class what they think about it. (4) Wonder: Ask students independently write what they wonder is true about the relationship between circumference and radius, and how they might find the circumference of a circle (Note: This step can also be done as a “Think-Pair-Share” with a partner.). After students write something down, have them share with the class what they think about it. (5) Extension: Following class discussion, students could take time to record what they have learned from today’s lesson, and summarize in their own words how radius and diameter relate to the circumference of a circle. They could also record any questions they have about circumference that the day’s lesson brought up. Notes:
|
| Assessment | Formative Assessment:
Summative Assessment:
|


For Jordan and gregg popovich comments James never hit back, but just yesterday in the knight’s basketball stadium set aside a James training video, far look like illusions emerged both Owen, a carefully look just know is James
adidas ultra boost
Obviously, the right to occupy a team-high 21.6 shots of Michael Owen, but failed to hit as James scores, this let a person feel, Owen has become a “cancer” of the knight.But many fans also feel,
nike air presto
Just wanna remark on few general things, The website design and style is perfect, the articles is rattling fantastic :D.
stephen curry shoes
Thanks for your post. I have continually noticed that the majority of people are eager to lose weight as they wish to look slim plus attractive. Having said that, they do not generally realize that there are additional benefits so that you can losing weight also. Doctors assert that fat people experience a variety of conditions that can be perfectely attributed to their own excess weight. The good news is that people who are overweight in addition to suffering from numerous diseases can reduce the severity of their own illnesses by way of losing weight. It is possible to see a slow but noted improvement with health when even a slight amount of weight-loss is reached.
adidas eqt
We have 24 states now that are members.
Cheap Authentic Jerseys
Obviously, the right to occupy a team-high 21.6 shots of Michael Owen, but failed to hit as James scores, this let a person feel, Owen has become a “cancer” of the knight.But many fans also feel,
curry 4
Draft of the same year on the bottom rookie will be what?In general the draft should be able to blow the other party, who would have thought them took Owen on the 60th pick small Thomas in the same year, he turned out to be in the position of the challenger?
kyrie 3 shoes
Derek Carr needs a wideout capable of separating from coverage and taking the lid off a defense.
Cheap NFL Jerseys China
Bradford – MTV Strategies | EDT 622
qyrmvszi http://www.g9cc1l8x403inc1l1031hstxxx3408f9s.org/
[url=http://www.g9cc1l8x403inc1l1031hstxxx3408f9s.org/]uqyrmvszi[/url]
aqyrmvszi
Steph, Amazing ideas within both MTV lessons. Just curious- what are some misconceptions that students have regarding exponents? I deal with misconceptions in science all the time and am just wondering about math misconceptions.
The video with the hamburger ordering is PERFECT for the lesson you created. I literally was “laughing out loud”- and am sure it would bring your lesson to a place that your students can really relate to as well.
Per your response about making connections…. you are so right because without helping students make their own connections… learning doesn’t really occur. The information becomes static instead of active and is not transferable.
Dr. MacKenzie, thank you for the feedback! Students often times struggle to know when exponents need to be added versus multiplied (this depends on whether you are multiplying two exponents with the same base, versus if you are taking a power to another power). They also get confused how to multiply their normal numbers in an expression when exponents are thrown into the mix, and how distributing applies to exponential expressions. A lot of these misconceptions stem from students forgetting that an exponent really just means repeated multiplication. They sometimes try to keep track of rules rather than truly understanding the process.
Steph,
I love your first lesson! It is really interesting to see that combining exponents is taught in middle school, yet it is something that I find myself (very) often reminding students about in algebra 2, precalc, and calculus. That video about combining like terms is hilarious!! And I love your ideas about the extending the activity to involve the students in creating their own cards. Taking this a step further, could students create a sets of non-examples as a way of “tricking” whoever is using them? This could provide an opportunity for further analysis of the information in a way that shows that they understand what looks like it could work but doesn’t (hopefully helping them to not make those mistakes in the future).
Hey Steph,
Awesome lessons. I think you did a great job picking out the specific learning routines to go with each topic. I especially like how you incorporated ‘See-Think-Wonder’ into your second activity. I think often times we don’t give students enough time to just look at something and think about it, without discussing it at all with anybody.
A couple of questions:
– What kinds of thoughts do you expect some students to write down about the 3 circles initially?
– Are your 7th graders capable of generating the formula on their own, or do they usually rely on collaboration?
You could also use this GeoGebra sketch (https://www.geogebra.org/m/fAMRfYk6) to conduct this lesson as well. Instead of having students only look at the 3 circle you gave them, they can generate their own. Probably not necessary, but may be more helpful for the hands-on learners.
Like I said, great job! I enjoyed reading through your lessons.
Steph, I love your exponents lesson. Although your lesson is designed for 7th and 8th graders, I think it would be an awesome refresher lesson for my 9th grade Algebra I students as well. You’ve really thought through all of the aspects of student engagement and having the students take ownership of their on concept development. The way you remind students of what a simplified expression is vs non simplified expression is awesome. If you wanted to keep it within the math realm, you could remind students by using linear expressions with combined like terms and non-combined like terms, or expanded order of operations problems in comparison to the simplified expression. (Of course I love the ice cream example too!)
I also really like your extension to the second lesson with students summarizing the relationship they found between radius and diameter. Great lessons, Steph!
Amy, thanks for the feedback. I like your idea of comparing the exponential expressions to other types of expressions and order of operations problems. Students seem to always struggle making connections between what they see in exponential expressions and what they have practiced before with order of operations and linear expressions. The more connections I can help students make between these concepts, the more likely students are to understand how all of these types of problems fit together. This could lead to such a deeper level of understanding for students.