CBCI – Frydryk

Unit Title:  Trig Functions:  Circles, Triangles, and Graphs – Oh My!
Conceptual lens: relationships
Unit strands: radians, unit circle, graphing sine & cosine
Topics & concepts:
– Radians – radian, circle, arc length, pi, radius
– Unit circle – radius = 1, right triangles
– Graphs – right triangles, unit circle, sine, cosine, (amplitude, frequency, period, translations?)
Generalizations and Guiding Questions:
– UNIT:  The graphs of sine and cosine, measured in radians, are generated from special right triangles drawn in the unit circle.
– LESSON 1:  Radians measure angles by relating the radius of a circle to the arc length of a central angle.
What do radians measure?
How do radians relate to the circumference formula?
How are radians related to circles?
– LESSON 1:  An angle that measures one radian has an arc length of one radius.
What is a radian?
How many radians is 180°? (or any other angle measure)
Is it better to use radians or degrees to measure angles?  Why?
– LESSON 2:  Special right triangles (30-60-90 and 45-45-90) with hypotenuse length 1 can be used with the unit circle to represent various central angle measures around the circle.
How can a 30-60-90 triangle be used to represent a 210° = 7π/6 angle? (or any other angle measure)
– LESSON 2:  Special right triangles in the unit circle give the (x,y) coordinate points of f(x) = sin x and f(x) = cos x, where x corresponds to the central angle and y corresponds to the sine or cosine value of that angle.
What are sine and cosine?
How does the unit circle help us understand the graphs of f(x) = sin x and f(x) = cos x?
How do triangles help us understand the graphs of f(x) = sin x and f(x) = cos x?
Critical content:
– LESSON 1:  definitions of radian and arc length, formula for the circumference of a circle
– LESSON 2:  unit circle values (sine, cosine, tangent of various angles), identify the graphs of sine and cosine
Key skills:
– LESSON 1:  calculate radian measure of an angle, convert angles from degrees to radians and vice versa
– LESSON 2:  geometrically portray the sine or cosine value of any angle on the unit circle. accurately sketch the graphs of sine and cosine.
Culminating assessment:  sample questions include:
– LESSON 1:  Geometrically portray, and explain in writing, why 210° = 7π/6
– LESSON 2:  Geometrically portray, and explain in writing, why sin (7π/4) = -√(2)/2
Suggested learning experiences: 2 outlined below are Radian Strings and Spaghetti Graphs
Unit overview:  Circles, triangles, and graphs are three seemingly unrelated mathematical ideas, yet they are intricately related once trigonometry is introduced.  In this unit we will explore the relationships between circles, triangles, and graphs of trigonometric functions.

Radian Strings
Overview:  In this lesson, students will look at how radian measure works/where it comes from, using a hands-on activity.Prior Knowledge Needed/When to Teach:  Students should be familiar with:  measuring the radius of a circle, the value pi
Timing: 1-2 days
Standards:
F-TF.A.1  Understand radian measure of an angle as the length of the arc on the unit circle subtended by the angle.
Materials:

• student circles
• string
• scissors

Outline:

• 3-4 different sizes of circles will be passed out to different pairs of students.
• Students will use the string to measure the radius of the circle (the center of the circle is marked), and cut a piece of string the length of the radius.
• Starting with a mark on the circumference of the circle, students will measure how many radius lengths it takes to “travel” around the entire circle.
• A discussion in small groups, then as a class, will clarify/ensure that all students found that around 6 to 6.5 radius lengths covers the entire circumference (the class average can also be calculated if desired to help with the accuracy of measurements).
• Teacher question, students discuss in small groups: “what do you know about the circumference of a circle? How does this connect to what you just did?”
• The connections between the circumference formula being 2πr, 2π ≈ 6.3, 6.3 being close to the number of radii they found that it takes to travel around the circumference, and r (from the equation) literally representing the radius of the circle are desired to be made
• A discussion about measuring angles in degrees versus radians will ensue, specifically regarding the concept behind degrees and radians (i.e. what is a radian? What is a degree? Degrees are a made-up measurement! Benefits/drawbacks of using each to measure angles).

Assessment:  For an exit ticket, homework, or entry ticket the next day, ask students to write a headline that includes the connections they saw during this activity regarding the terms:  radian, circle, arc length, pi, radius, angle

What components of CONCEPT-BASED CURRICULUM AND INSTRUCTION play out in your post?
This lesson gives students the opportunity to create their own generalizations, hopefully aligning with a few of the generalizations set out for the unit, after exploring the concept of radian measure.  The students are literally constructing what radian measure means by measuring the radius of a circle and connecting this to central angles.
There are facts that students are asked to know:
definitions of radian, arc length
formulas for the circumference of a circle
There are concepts that students are asked to understand:
Radians measure angles by relating the radius of a circle to the arc length of a central angle.
An angle that measures one radian has an arc length of one radius.
There are skills that students are asked to be able to do:
Calculate radian measure of an angle.
Convert angles from degrees to radians and vice versa.

Spaghetti Graphs
Overview:  In this lesson, students will make connections between calculating the sine, cosine, and tangent values for a right triangle and how this directly relates to the graphs of functions f(x) = sin x and f(x) = cos x.
Prior Knowledge Needed/When to Teach:

• radian measure
• how to calculate sine and cosine for a triangle
• familiar with unit circle and positive/negative reference angles

Timing:  2-3 days
Standards:
F-TF.A.3  Use special triangles to determine the values of sine, cosine, tangent for pi/3, pi/4, pi/6, and use the unit circle to express the values of sine, cosine, and tangent for x, pi+x, 2pi-x in terms of their values for x, where x is any real number.
Materials:

• butcher paper (for See, Think, Wonder)
• unit circles with reference angles given
• large graph paper for graphing sine and cosine
• Pull-n-Peel Twizzlers

Outline:

• Pull up this Geogebra sketch that shows students an animation of how the graphs of sine, cosine, and tangent connect to the unit circle.
  • Give students 2-3 minutes to individually write down what they SEE.
  • Give students 2-3 minutes to individually write down what they THINK.
  • Give students 1-2 minutes to individually write down what they WONDER.
• In pairs, give students 3 minutes to discuss what they wrote down. Each pair of students will pick out one comment for each category to write on the butcher paper in the front of the room.
  • Discuss as needed (any comments that will drive the activity, questions that stand out, etc.).
• Students work in pairs with a full-page unit circle (with reference points), two pieces of full page graph paper, and multiple Pull-n-Peel Twizzler strands.
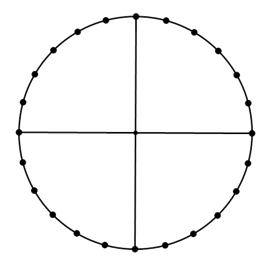
• Explain the purpose of the activity: we want to understand where the graphs of f(x) = sin x and f(x) = cos x come from, and how they relate to triangles
• Discuss/review in small groups (teacher prompts given in questions and parentheses)
  • the measurement units of the axes on the graph paper and what they represent
  • connections between the graph paper and the unit circle (units, measurements, sine/cosine/triangles)
  • how drawing special right triangles in different places in/on the unit circle changes what is being assumed/measured
  • plot multiple/enough points on the sine/cosine graph to create an accurate picture (how many points is enough?)
  • What to do about triangles that are “upside-down” on the unit circle? (may give negative sine/cosine values)
  • When will negative sine/cosine values be seen on the unit circle?
• Together, label the axes on the sine and cosine graphs in both radians and angles, referencing the “Radian String” lesson as much as possible.
• Students draw a special right triangle on the unit circle, using one of the reference points given, with a segment drawn vertically down to the x-axis, and a segment drawn straight from the reference point to the center of the circle.
• Using that triangle, they determine the sine (or cosine) of that central angle (hypotenuse is 1 since it is a unit circle, so the sine (or cosine) is simply the length of the opposite (or adjacent) side length to the central angle).
• Students will break off a piece of Twizzler that matches the length of the side length for sine (or cosine).
• This piece of Twizzler is then used to mark the sine (or cosine) value of the angle on the corresponding x = θ line of the graph, where θ is the central angle that was used to draw the triangle.
• This process is repeated all the way around the unit circle (students should start to see patterns/repetition in the measurements, so they may not actually need to draw/measure each individual triangle/angle).
• The resulting graphs (should) give a sketch of the sine and cosine curves.
• Review the See, Think, Wonder comments from the beginning of the lesson. Students discuss what they learned, questions that were answered, thoughts/assumptions that were correct, etc.

Assessment:
Students will respond to two journaling prompts:
How does the unit circle help us understand the graphs of f(x) = sin x and f(x) = cos x?
How do triangles help us understand the graphs of f(x) = sin x and f(x) = cos x?
Notes to Teacher:

• It may be helpful to pre-peel the Twizzlers in order to reduce waste and too much snacking 😊

What components of CONCEPT-BASED CURRICULUM AND INSTRUCTION play out in your post?
This lesson provides students with the opportunity to see, experience, and build the graphs of sine and cosine using special right triangles and the unit circle.
There are facts that students are asked to know:
Unit circle values (sine, cosine, tangent of various angles)
Identify the graphs of sine and cosine
There are concepts that students are asked to understand:
Special right triangles (30-60-90 and 45-45-90) with hypotenuse length 1 can be used with the unit circle to represent various central angle measures around the circle.
Special right triangles in the unit circle give the (x,y) coordinate points of f(x) = sin x and f(x) = cos x, where x corresponds to the central angle and y corresponds to the sine or cosine value of that angle.
There are skills that students are asked to be able to do:
Geometrically portray the sine or cosine value of any angle on the unit circle.
Accurately sketch the graphs of sine and cosine.

For more information search Pinterest, TeachersPayTeachers, or Twitter (using hashtags) for:  trigonometry graphs, trig graphs, radians, unit circle