Viscoelastic Materials: Introduction

Some materials such as polymers, ceramics, rubbers, woods etc. exhibit a time/rate dependent stress-strain relationship. These materials are categorized as being visco-elastic, which implies the combined presence of deformation characteristics associated with elastic (typically metallic) solids and viscous fluids. Consider, first, purely elastic behavior. The loading and unloading stress-strain curves of a linear elastic material $(\sigma =E\varepsilon$ .) are identical, implying no hysteresis, as shown in Fig. 1a. Furthermore, the elastic nature of the deformation implies that there is no residual strain in the material upon complete unloading and that the loading rate does not affect the stress-strain curve. The deformation of an elastic solid results in the accumulation of internal strain energy, which can be fully recovered as the external load is removed.

On the other hand, the deformation behavior and the accompanying nature of the exchange of energy are quite different in the case of viscous materials. When an external load/stress is applied, ideal fluids ( $\tau =\eta \dot{\gamma}$ ) do not retain the work done as stored energy but rather continuously dissipate energy. The applied stress varies in response to the deformation rate, with higher deformation rates typically requiring more stress. Viscoelastic materials embody elastic solids and fluid characteristics by exhibiting non-linear, hysteretic, and rate-dependent deformation behavior. As seen in Fig. 1b, there is partial recovery of the work done on the material, as evidenced by the area between the loading and unloading curves, i.e., hysteresis. The study of viscoelasticity encompasses such a time-dependent phenomenon, and the deformation response of common polymeric materials will be used to highlight these characteristics through tests investigating rate dependence, creep, and relaxation. Fig 1. (a) Illustration of the linear elastic behavior with full energy recovery, (b) Non-linear viscoelastic behavior (rate dependent: ), and (c) viscoplastic behavior.

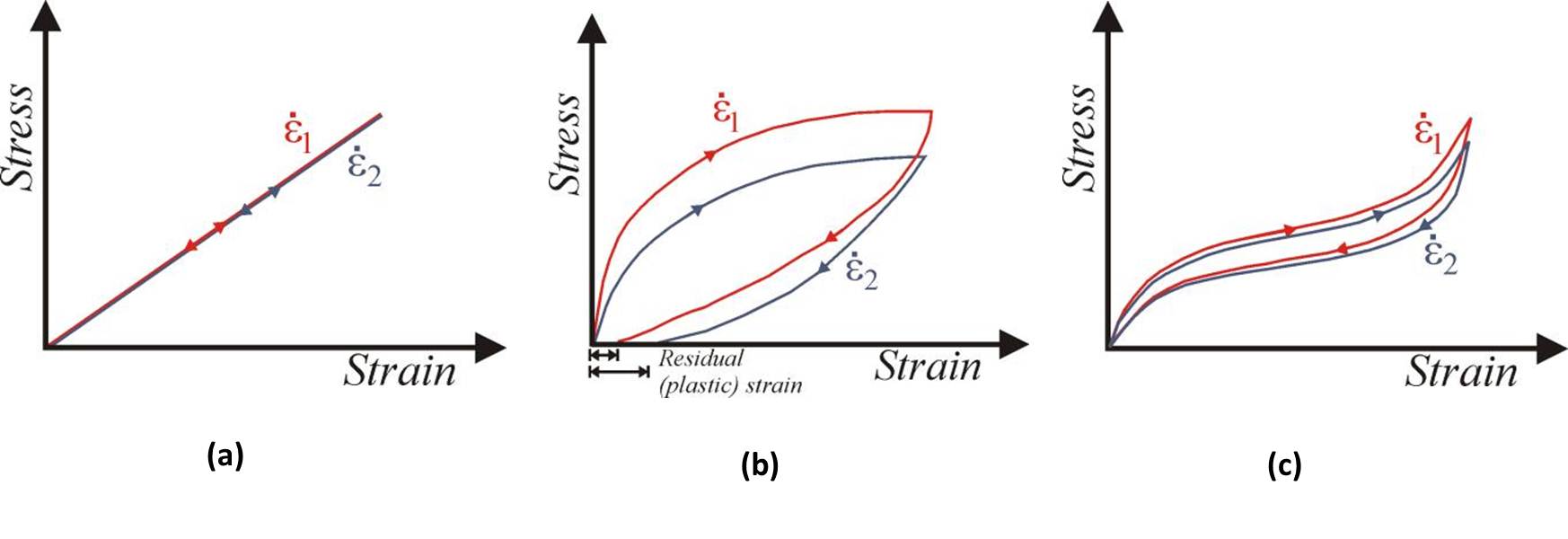
Fig 1. (a) Illustration of the linear elastic behavior with full energy recovery, (b) Non-linear viscoelastic behavior (rate dependent: ), and (c) viscoplastic behavior.

Creep: This phenomenon refers to an increase in strain over time when a condition of constant (non-zero) stress is maintained (Input: constant stress → Output: change in strain). Creep occurs due to the fact that molecular chain motions such as rotation, sliding, and disentanglement take finite time to occur. This is a manifestation of the viscous nature of polymeric materials. The accumulation of creep strain can be predicted through creep compliance, which is the ratio of time-varying strain $\varepsilon (t)$ , to the applied constant instantaneous stress $\bar{\sigma }$ .

Creep compliance: ${{J}_{creep}}=\frac{\varepsilon(t)}{{\bar{\sigma}}}$

Relaxation: As the name implies, this behavior refers to a decrease in the stress sustained by a material under the condition of constant strain (Input: constant strain → Output: change in stress). The loss in tension in racquet strings and nylon guitar strings over time are examples of stress relaxation. The specific protocol for a relaxation test entails loading to a target stress/strain point, following which a condition of constant strain is immediately implemented. Typically, the rate of change of stress is initially large and approaches zero over longer time frames. The origin of stress relaxation can be understood on the basis of chain motion, which allows long molecules to rotate and slide into new configurations and alleviate the overall stress sustained by the material. Recall that these mechanisms for chain mobility are responsible for the viscous, i.e., time-dependent, deformation characteristics of polymers. The stress change is quantified by calculating the relaxation modulus, which is the ratio of time-varying stress $\sigma(t)$ , to the applied constant instantaneous strain $\bar{\varepsilon}$ .

Relaxation modulus: ${{E}_{relax}}=\frac{\sigma (t)}{{\bar{\varepsilon }}}$

Rate Dependence: Even in the absence of a specialized test such as creep or relaxation, perhaps the most frequently encountered manifestation of viscoelasticity is rate dependence, or more specifically, positive strain rate sensitivity. A faster rate of deformation produces a higher stress-strain curve, see Fig. 1b and 1c, and this property is a direct consequence of the viscous nature of polymeric materials. The increase in stress is typically non-linearly related to the strain rate used for loading.

<< Learning Module Objective Viscoelastic Material: Importance >>

Polymer Learning Moudule

Characteristics of Viscoelastic Materials

Viscoelastic Materials: Introduction